Предлагаем вам вариант еще одной новой и увлекательной игры, которая подойдет как детям, так и взрослым. На первый взгляд, она представляет собой типичную головоломку с переменными начальными условиями типа кубика Рубика, судоку или пасьянса. Однако ее возможности значительно шире.
Предлагаем вам вариант еще одной новой и увлекательной игры, которая подойдет как детям, так и взрослым. На первый взгляд, она представляет собой типичную головоломку с переменными начальными условиями типа кубика Рубика, судоку или пасьянса. Однако ее возможности значительно шире.
Антонио Грамши
Игра в конфигурации может использоваться как конструктор для разнообразных красивых конфигураций — аналогично игре (точнее, клеточному автомату) «Жизнь», — а также для создания интересных математических задач.
Правила игры очень просты. На «бесконечном» листе бумаги в клетку задается произвольная начальная конфигурация из конечного числа крестиков, которую назовем затравкой. Пример затравки представлен на рис. 1.
Рисунок 1 Назовем приведенную на рисунке затравку из четырех крестиков тетрадой. Здесь и в следующих рисунках затравка выделена синим цветом.
К затравке последовательно добавляются новые крестики в соответствии со следующими двумя правилами.
- Каждый выставляемый крестик должен образовывать с уже выставленными хотя бы один ряд из трех рядом стоящих крестиков по вертикали, горизонтали или диагонали. Из этого правила следует, что нельзя выставлять изолированный крестик, а также выстраивать ряд, состоящий лишь из двух рядом стоящих крестиков.
- Запрещается ставить крестик, если он при этом образует с уже выставленными хотя бы один ряд более чем из трех рядом стоящих крестиков. Эти правила иллюстрируются на рис. 2.
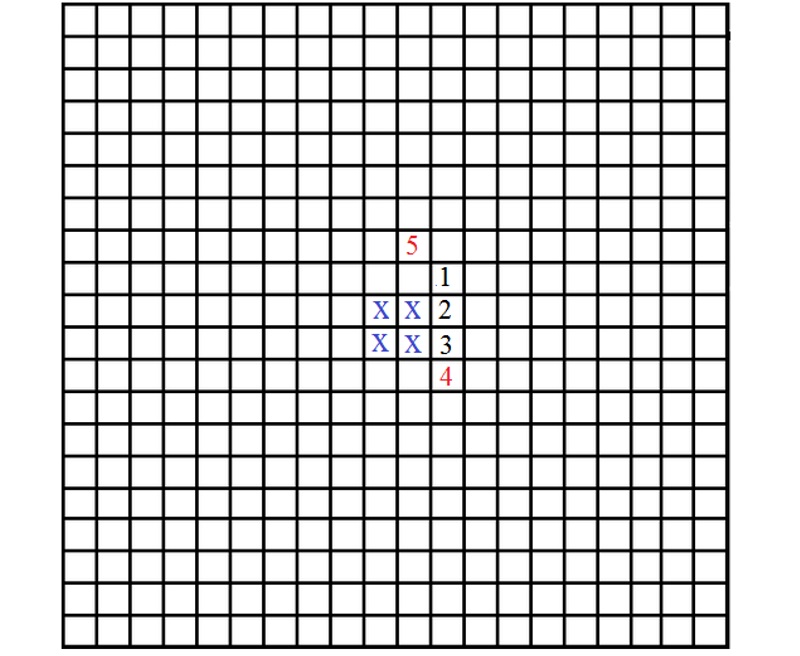
Рисунок 2 В клетки 1, 2, 3 ставить крестики можно. После этого в клетку 4 крестик ставить нельзя, т.к. образуется ряд из четырех рядом стоящих по вертикали крестиков [1, 2, 3, 4] (нарушено правило 2). В клетку 5 крестик тоже ставить нельзя, т.к. при этом образуется диагональный ряд лишь из двух крестиков [1, 5] (нарушено правило 1).
Оказывается, к любой затравке можно добавить лишь конечное число новых крестиков (бесконечные затравки мы пока не затрагиваем). Попробуйте это доказать!
Конфигурации, к которым невозможно, не нарушая правил, добавить новые крестики, назовем полными. В противном случае они считаются неполными. Некоторые полные конфигурации, порожденные тетрадой, обладают изящной симметричной структурой (рис. 3 — 6).
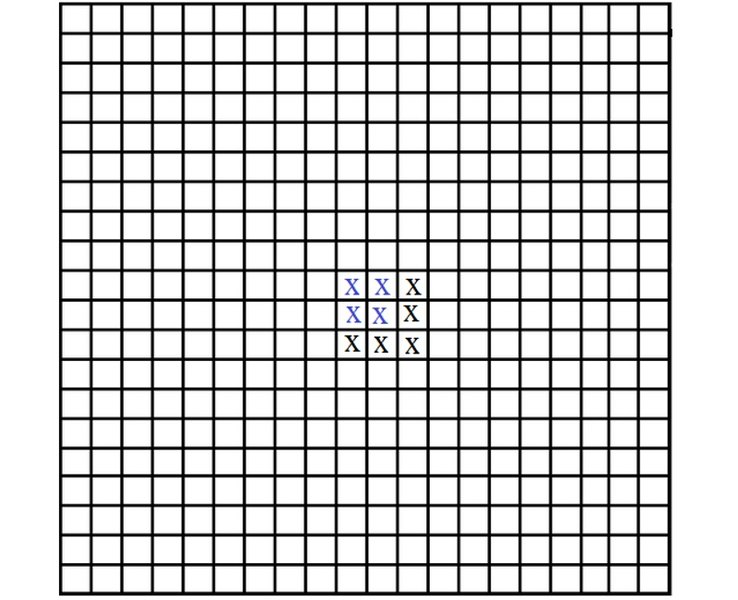
Полная конфигурация из 9 крестиков.
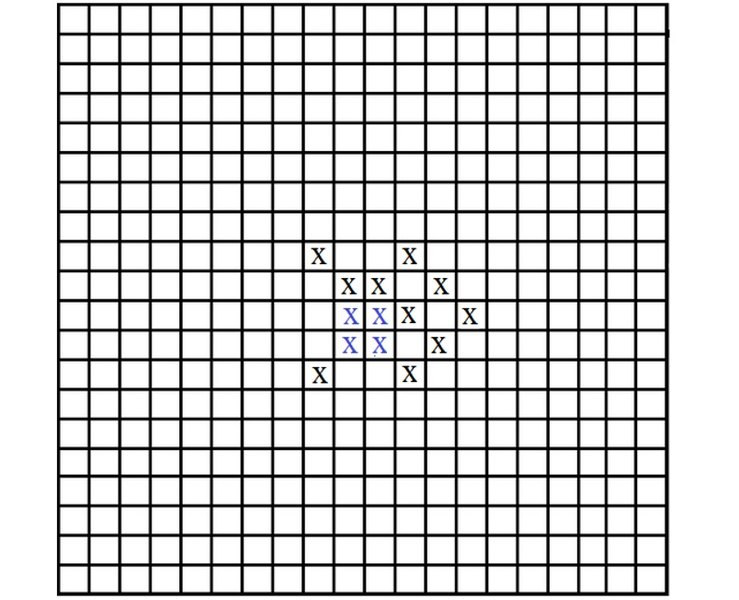
Полная конфигурация из 12 крестиков. Ее симметричность нарушена нижним левым крестиком тетрады. Тем не менее, конфигурация воспринимается как правильная. Это связано с тем, что она получена двумя последовательными параллельными переносами конфигурации из четырех крестиков. Какой?
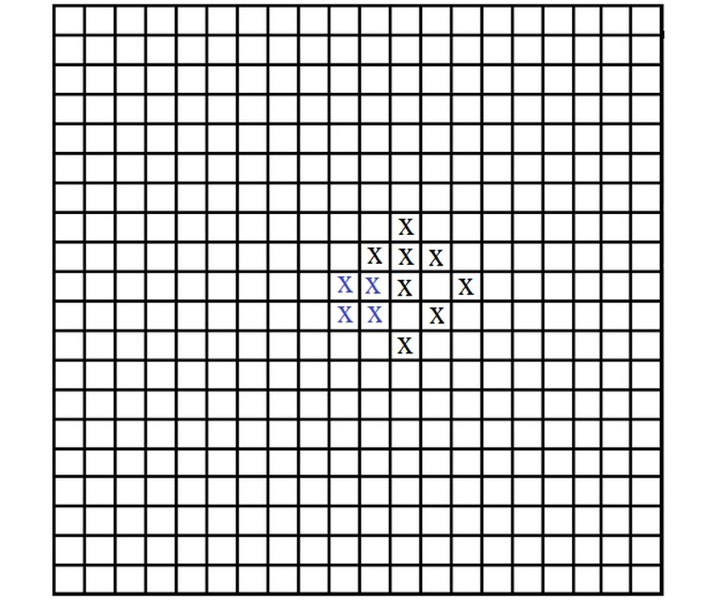
Полная конфигурация из 14 крестиков.
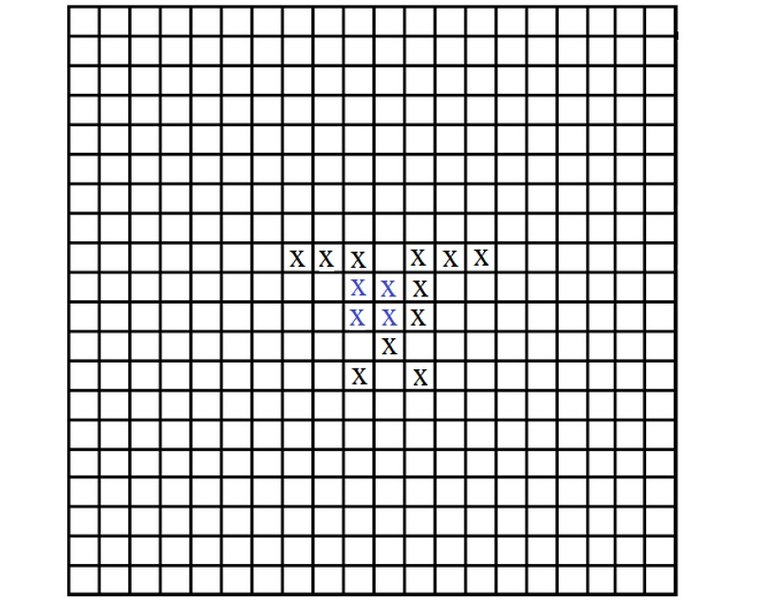
Полная конфигурация из 15 крестиков.
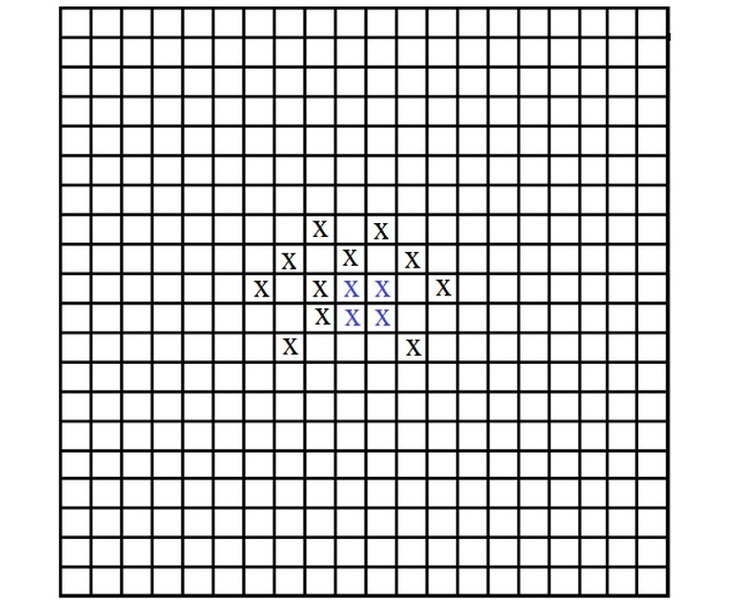
Еще одна полная конфигурация из 15 крестиков.
Конечность полных конфигураций естественным образом определяет несколько взаимосвязанных классов задач, которые и можно считать целями игры. Приведем некоторые из них.
1. Для заданной затравки найти полную конфигурацию с максимальным числом крестиков. В общем случае эта задача сложна (пока не найдено разумного алгоритма, не сводящегося к простому перебору возможностей). Автор предполагает, что к тетраде можно добавить, самое большее, 19 новых крестиков. Соответствующая полная конфигурация из 23 крестиков изображена на рис. 8.
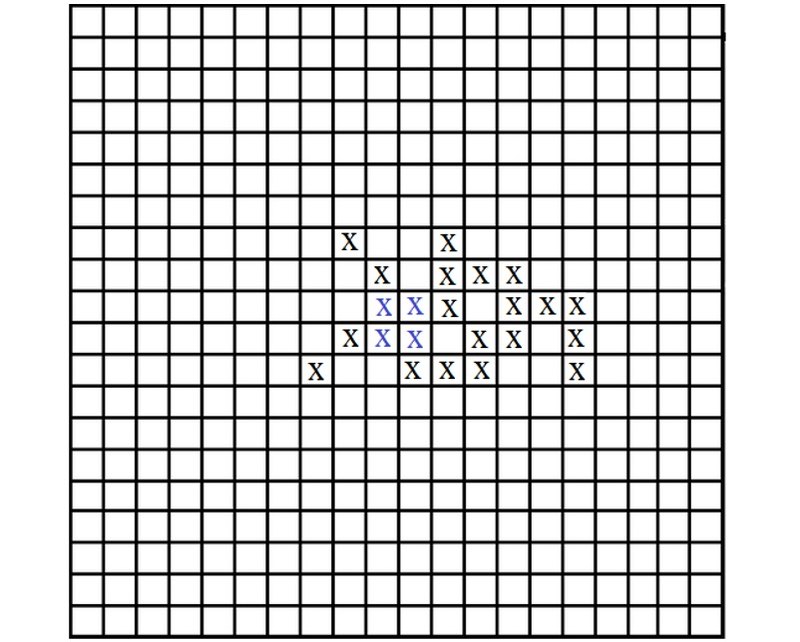
Рисунок 8 Восстановите последовательность ходов, ведущих к этой полной конфигурации.
Можно, наоборот, задаться целью найти для данной затравки минимальную полную конфигурацию. Для тетрады ею будет квадрат 3 3, изображенный на рис. 3. Число крестиков в нем равно 9.2. Для заданной затравки найти полную конфигурацию с фиксированным числом крестиков. Автору удалось найти порожденные тетрадой полные конфигурации с числом крестиков, равным 9, 11, 12, 13, 14, 15, 18, 20, 22 и 23. Попытайтесь самостоятельно найти их. Кстати, для числа 12 существуют как минимум три различные конфигурации.
Интересное в сети
3. Для заданной полной конфигурации найти порождающую ее минимальную затравку (то есть такую, которая состоит из минимального числа крестиков). Разумеется, при этом нужно отыскать и соответствующую последовательность ходов. Составление и решение задач такого рода может доставить подлинное эстетическое удовольствие. Приведем два примера. Найдите минимальную затравку для полной конфигурации, изображенной на рис. 9.
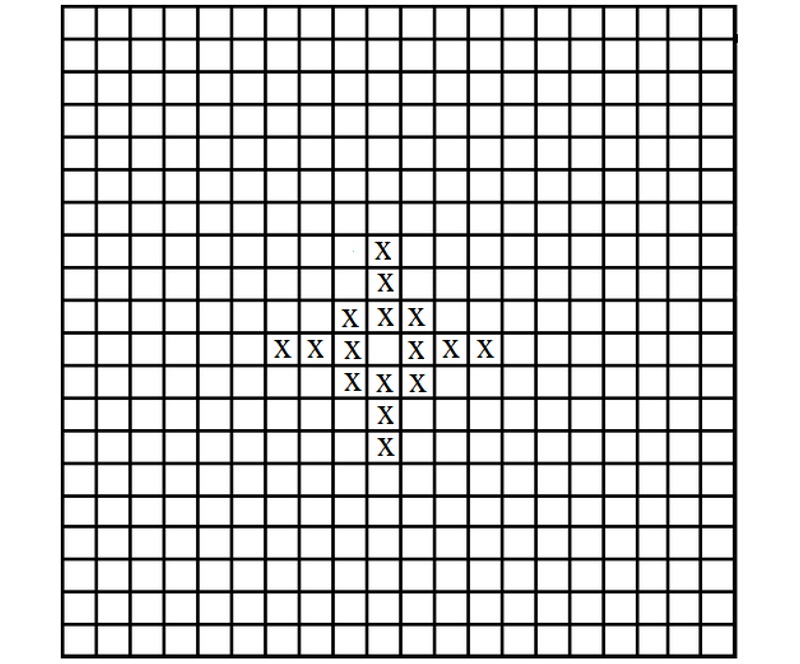
Рисунок 9
В качестве решения напрашивается затравка из четырех крестиков, обладающая тем же типом симметрии, что и конечная конфигурация. Однако задачу решают затравки с иным типом симметрии. Две из них изображены на рис. 10a и 10b.
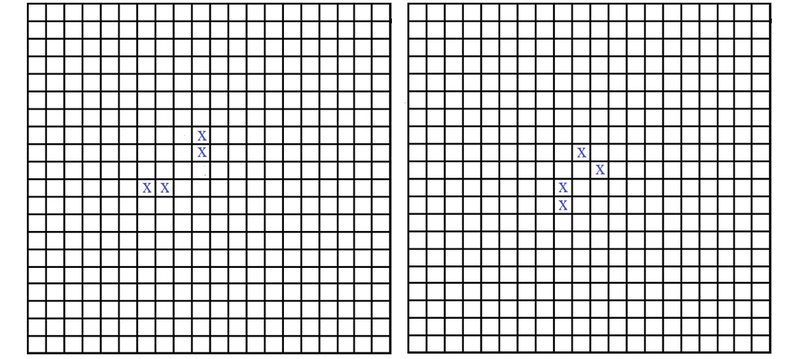
Рисунок 10a и 10b
Решите аналогичную задачу для полной конфигурации, изображенной на рис. 11.
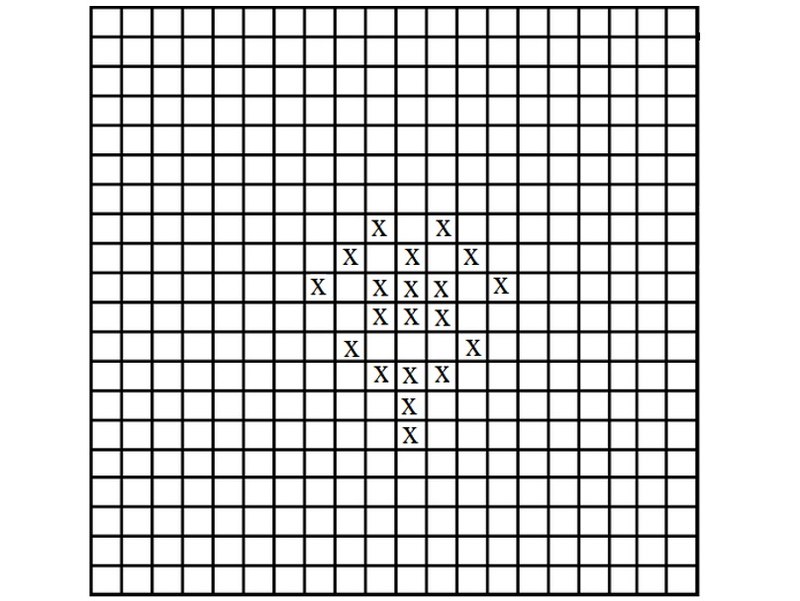
Рисунок 11
Минимальное количество крестиков в затравке для этой конфигурации равно 5. Два варианта решения представлены на рис. 12a и 12b.
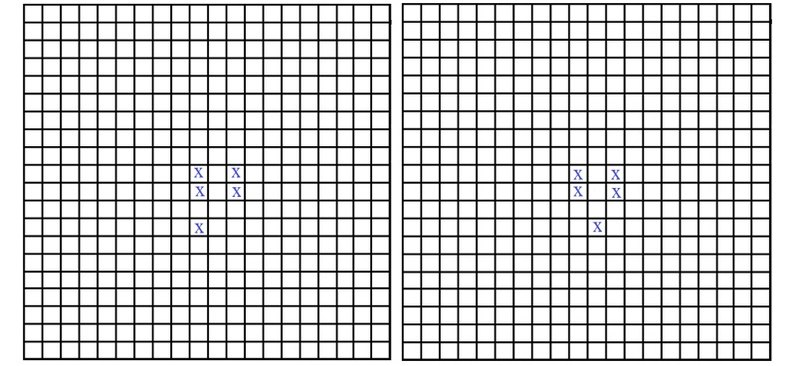
Рисунок 12а и 12b
Полные конфигурации могут быть использованы в качестве элементов декора. Их главное эстетическое достоинство — ажурность. На рис. 13 приведены симметричные полные конфигурации, полученные из тетрады, представленные в виде цветной мозаики.
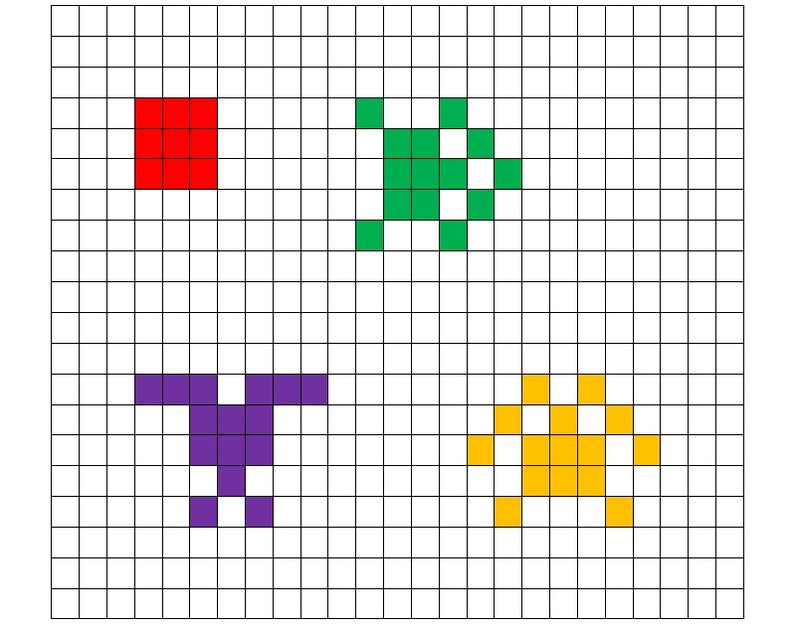
Рисунок 13
Назовем такую мозаику эквидистантной (от лат. equus — равный, distantia — расстояние). Это означает, что любой отрезок, соединяющий центры выставленных квадратиков и целиком принадлежащий им, не превышает фиксированной величины, выраженной в условных метрических единицах, в данном случае трех единиц. Подразумевается так называемая шахматная метрика, в которой сторона квадрата равна его диагонали. Представим в виде цветной мозаики полные конфигурации из последних двух задач (рис. 14).
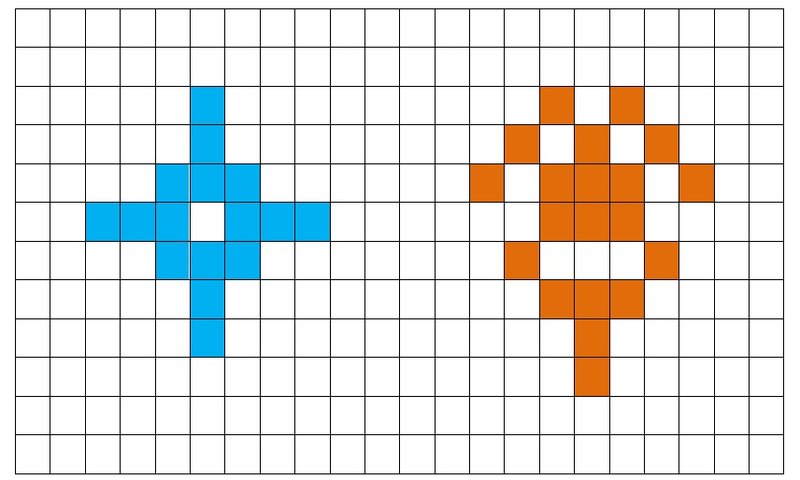
Рисунок 14
Теперь используем голубую фигуру слева в качестве повторяющегося элемента — мономера — бесконечной цепи, которая, в свою очередь, образует полную конфигурацию (рис. 15).
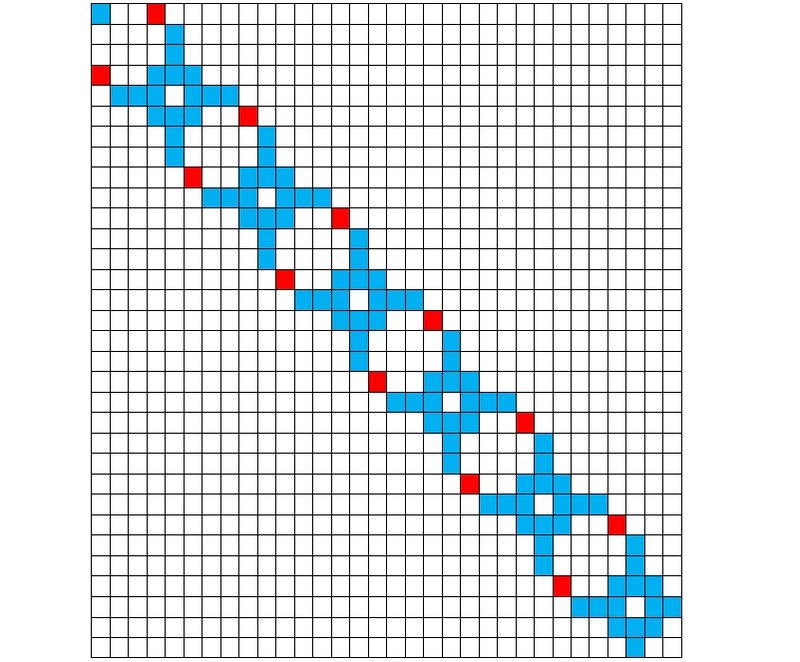
Рисунок 15 Цепь идет в направлении от левого верхнего угла в нижний правый. Изображен ее конечный фрагмент. Красным цветом выделены квадратики, которые после соединения мономеров в цепь добавлены для того, чтобы конфигурация стала полной.
Присоединим с левой стороны полученной цепи ее копию так, чтобы в результате тоже получилась полная конфигурация (рис. 16).

Рисунок 16 Желтым цветом выделены квадратики, которые после соединения цепей добавлены для того, чтобы конфигурация стала полной.
Ясно, что продолжая процесс присоединения цепей слева, можно заполнить всю плоскость (рис. 17).

Рисунок 17
Считая белые квадратики элементами мозаики, получим замощение плоскости. Полученное нами замощение обладает разнообразными элементами (видами) симметрии. Сможете их перечислить?
Интересное в сети
Мы намеренно использовали усложненное соединение мономеров в цепь — через красный квадратик, — чтобы получить нетривиальное замощение с богатым набором симметрий. Разумеется, можно было соединить мономеры более простым способом. Каким? Постройте соответствующее замощение. С помощью аналогичной процедуры, проведенной над другими полными конфигурациями, можно получить новые интересные мозаики.
Найдите красивые решения!











Спасибо!
Теперь редакторы в курсе.